Programmers ] Level 2 - 멀쩡한 사각형

 

 

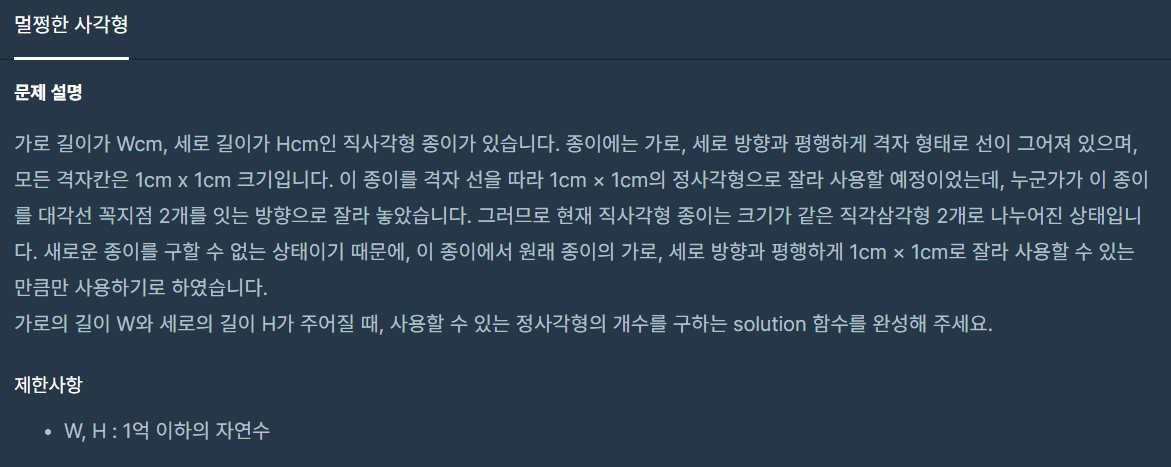
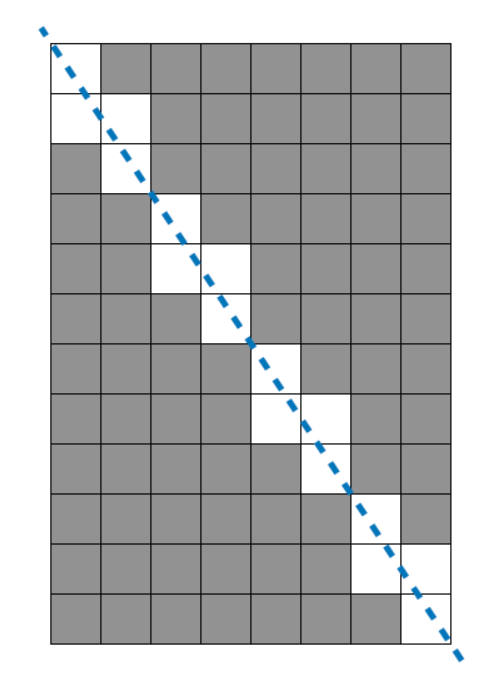
도무지 로직이 생각나지 않았다.

처음엔 하드 코딩으로 해결했으나 테스트 케이스는 맞았고, 실제 채점 결과... 하나만 정답 처리됐다.

 

이런 식으론 풀이가 안 될 것 같아서 여러 가지 케이스의 사각형을 직접 그린 후, 규칙을 찾으려고 했다.

그러자 아래와 같은 두 가지 경우가 있다는 것을 발견했다.

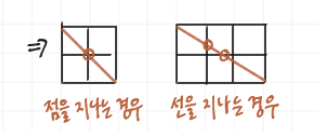
그러나 아무리 생각해봐도 다음 풀이 방법으로 넘어갈 수 없었다.

진척이 없었다..

다른 문제 풀이 방법과 달리 수학적 사고가 필수 불가결한 문제라고 판단됐다.

 

그래서 다른 사람의 풀이 과정을 참고하며, 내 사고력을 확장시키고 싶었다.

참고용으로 유투브에서 문제 풀이까지 사고하는 과정을 따라해보기로 했다.

 

 

🧩 문제 접근 방법 

*접근 방법은 해당 동영상 해설자분을 따라 해보았습니다 *

 

1. w, h의 최대공약수를 활용하면 어떨까?

위 그림을 보면, 같은 도형이 반복되고 있다.

반복되는 도형

 

위 도형은 총 4개가 발견되고, w = 8과 h = 12의 최대공약수 또한 4이다.

따라서 최대공약수를 활용하면 규칙을 발견할 수 있지 않을까? 라는 생각을 해보았다.

 

 

2. 점과 선을 지나는 점선

 

위 그림을 보면 선을 지날 때는 2개의 도형이, 점을 지날 때는 1개의 도형을 사용한다.

 

 

>> 따라서 

	h는 총 12이다.
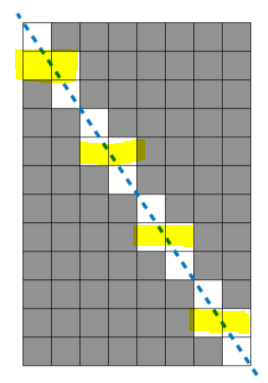	노란색으로 체크된 도형을 보면 칸 마다 2개씩 체크가 된다. 그렇다면 나머지 흰색 도형은 어떻게 체크할 수 있을까?
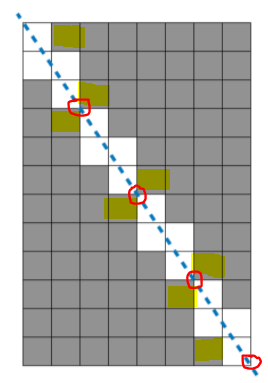	점선이 두 개의 정삼각형의 점을 4번 지나간다. 만약 왼쪽 그림에서 노란색으로 체크된 부분까지 2개씩 체크가 된다면 12 * 2 = 24. 하지만 24에서 노란색 정사각형을 빼줘야 하므로 24 - 8 = 24 - (4 * 2)             = 24 - (점선이 점을 지날 때 count * 2)             = h * 2 - (최대공약수 * 2) 따라서 w * h - ( h * 2 - 최대공약수 *  2)라는 로직을 발견했다.
다시 한 번 아래와 같이 정리했다. w * h - ( h * 2 - 최대공약수 *  2) == w * h - w - h + 최대공약수

 

 

🌱 정답코드